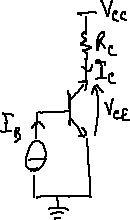Sistemi e tecnologie elettroniche/Il transistore bipolare
2 Il transistore è un dispositivo elettronico caratterizzato da:
- almeno tre terminali, uno dei quali individua il terminale comune tra la porta[1] di ingresso e la porta di uscita;
- una corrente di uscita <math>I_u</math> che dipende, oltre che dalla tensione di uscita <math>V_u</math>, anche dal segnale di ingresso:
- transistore bipolare: (analogico) la caratteristica di uscita <math>I_u \left( V_u,I_i \right)</math> è controllata in corrente <math>I_i</math>;
- transistore a effetto di campo (FET): (digitale) la caratteristica di uscita <math>I_u \left( V_u,V_i \right)</math> è controllata in tensione <math>V_i</math>.
I transistori trovano applicazione nei generatori pilotati, negli amplificatori, nei circuiti digitali... Per le leggi di Kirchhoff:
- <math>\begin{cases} I_1 + I_2 + I_3 = 0 \\ V_{21} = V_2 - V_1 = V_{23} - V_{13} \end{cases}</math>
5 Il transistore bipolare a giunzione è un dispositivo caratterizzato da tre terminali detti emettitore, base e collettore, che corrispondono alle tre regioni ottenute unendo due giunzioni pn in antiserie.
Regioni di funzionamento[modifica | modifica sorgente]
6 A seconda della polarizzazione delle due giunzioni, si hanno quattro regioni di funzionamento:
- regione attiva diretta: giunzione BE in diretta (<math>V_{BE} >0</math>), giunzione BC in inversa (<math>V_{BC} <0</math>);
- regione attiva inversa: giunzione BE in inversa (<math>V_{BE} <0</math>), giunzione BC in diretta (<math>V_{BC} >0</math>): le prestazioni da amplificatore sono pessime perché il transistore bipolare non è ottimizzato in termini di livelli di drogaggio per lavorare in regione attiva inversa;
- regione di interdizione: giunzione BE in inversa (<math>V_{BE} <0</math>), giunzione BC in inversa (<math>V_{BC} <0</math>): approssima il circuito aperto (<math>I_C \approx I_E \approx 0</math>) perché i portatori maggioritari non sono spinti dall'emettitore al collettore;
- regione di saturazione: giunzione BE in diretta (<math>V_{BE} >0</math>), giunzione BC in diretta (<math>V_{BC} >0</math>): approssima il cortocircuito perché la caduta di potenziale è trascurabile (<math>V_{CE} = V_{BE} - V_{BC} \approx 0</math>) con un forte flusso di corrente.
7 Le regioni attive sono usate per le applicazioni analogiche, le altre due per le applicazioni digitali.
Regione attiva diretta[modifica | modifica sorgente]
Uso come amplificatore (analogico)[modifica | modifica sorgente]
3-4 Si collegano un generatore di corrente <math>I_i</math> e una resistenza di carico <math>R_c</math> a un transistore che lavora in condizioni di piccolo segnale. Un amplificatore richiede una relazione lineare tra ingresso e uscita:
- <math>\begin{cases} I_u \left( V_u , I_i \right) = I_u \left( {V_u}_0 + {v_u}_{ss} \left( t \right) , {I_i}_0 + {i_i}_{ss} \left( t \right) \right) \simeq I_u \left( {V_u}_0 , {I_u}_0 \right) + {\left. \frac{\partial I_u}{\partial V_u} \right|}_{\left( {V_u}_0 , {I_u}_0 \right)} \cdot {v_u}_{ss} \left( t \right) + {\left. \frac{\partial I_u}{\partial I_i} \right|}_{\left( {V_u}_0 , {I_u}_0 \right)} \cdot {i_i}_{ss} \left( t \right) \\ I_u \left( V_u , I_i \right) = {I_u}_0 + {i_u}_{ss} \left( t \right) = I_u \left( {V_u}_0 , {I_u}_0 \right) + {i_u}_{ss} \left( t \right) \end{cases} \Rightarrow \begin{cases} {i_u}_{ss} \left( t \right) = {\left. \frac{\partial I_u}{\partial V_u} \right|}_{\left( {V_u}_0, {I_u}_0 \right)} \cdot {v_u}_{ss} \left( t \right) + {\left. \frac{\partial I_u}{\partial I_i} \right|}_{\left( {V_u}_0 , {I_u}_0 \right)} \cdot {i_i}_{ss} \left( t \right) \\ {i_u}_{ss} \left( t \right) = C \cdot {i_i}_{ss} \left( t \right) \end{cases} \Rightarrow \begin{cases} C= {\left. \frac{\partial I_u}{\partial I_i} \right|}_{\left( {V_u}_0 , {I_u}_0 \right)} \\ {\left. \frac{\partial I_u}{\partial V_u} \right|}_{\left( {V_u}_0 , {I_u}_0 \right)} \cdot {v_u}_{ss} \left( t \right) = 0 \Leftrightarrow I_u \left( V_u \right) = \text{cost.} \end{cases}</math>
Affinché sia un amplificatore, la caratteristica di uscita <math>I_u</math> deve dipendere da <math>V_i</math> ma non da <math>V_u</math>.
Descrizione qualitativa[modifica | modifica sorgente]
5 Per esempio, nel transistore npn:
- la tensione di polarizzazione diretta applicata sulla giunzione np a sinistra spinge gli elettroni liberi maggioritari dal suo lato n (emettitore) alla regione p (base) in comune con la giunzione pn a destra;
- se la base è abbastanza sottile (8 in particolare più corta della lunghezza di diffusione), gli elettroni non fanno in tempo a ricombinarsi ed entrano nella regione svuotata della giunzione pn a destra;
- la tensione di polarizzazione inversa della giunzione pn a destra li spinge verso il suo lato n (collettore), creando una corrente di trascinamento.
In questo modo, la corrente di trascinamento generata è molto più alta di quella che si otterrebbe da una giunzione pn isolata, perché ai portatori minoritari della giunzione pn a destra si aggiungono i portatori maggioritari provenienti dalla giunzione np a sinistra; per questo motivo, la corrente di trascinamento generata è fortemente dipendente dalla tensione di polarizzazione diretta applicata alla giunzione pn il cui lato n è l'emettitore, e viceversa per il collettore → il transistore bipolare è un amplificatore perché la corrente di uscita <math>I_C</math> è indipendente dalla tensione applicata sull'uscita <math>V_{CE}</math>.
8 Nonostante sia geometricamente simmetrica, la struttura del transistore bipolare non è simmetrica in quanto i livelli di drogaggio dell'emettitore e del collettore differiscono in modo che il transistore sia ottimizzato per lavorare in regione attiva diretta.
Descrizione quantitativa[modifica | modifica sorgente]
9 Le concentrazioni di portatori minoritari ai confini delle regioni di svuotamento seguono le leggi delle giunzioni:
- regione di svuotamento tra emettitore e base:
- <math>\begin{cases} p_n' \left( {x_E}^- \right) = \frac{ {n_i}^2 }{ {N_D}_E } \left( e^{\frac{V_{BE}}{V_T}} -1 \right) \\ n_p' \left( {x_E}^+ \right) = \frac{{n_i}^2}{ {N_A}_B } \left( e^{\frac{V_{BE}}{V_T}} -1 \right) \end{cases}</math>
- regione di svuotamento tra base e collettore:
- <math>\begin{cases} n_p' \left( {x_C}^- \right) = \frac{ {n_i}^2 }{ {N_A}_B } \left( e^{\frac{V_{BC}}{V_T}} -1 \right) \\ p_n' \left( {x_C}^+ \right) = \frac{{n_i}^2}{ {N_D}_C } \left( e^{\frac{V_{BC}}{V_T}} -1 \right) \end{cases}</math>
Poiché i bordi della giunzione sono dei contatti ohmici, non ci sono portatori minoritari in eccesso. Spesso l'emettitore e la base sono lati corti e il collettore è un lato lungo → gli eccessi di portatori minoritari hanno un andamento esponenziale nel collettore e lineare nella base e nell'emettitore → 10 le correnti di diffusione, legate alle derivate degli eccessi di portatori minoritari,[2] sono costanti nella base e nell'emettitore, ed esponenziali ma molto piccole nel collettore.
Il flusso <math>F</math> di portatori è il numero di portatori per unità di tempo e di area che si spostano:
- <math>\begin{cases} \left| {J_{\text{diff}}}_n \right| = q \left| F_n \right| \\ \left| {J_{\text{diff}}}_p \right| = q \left| F_p \right| \end{cases}</math>
11 In totale sono presenti 5 flussi di carica:
- <math>\begin{cases} I_E = -q A {F_n}_{EB} -qA {F_p}_{BE} \\ I_C = qA {F_n}_{BC} + \left( qA { {F_n}_{BC} }_0 + q A { {F_p}_{CB} }_0 \right) = qA {F_n}_{BC} + {I_{CB}}_0 \approx qA {F_n}_{BC} \end{cases}</math>
dove:
- la corrente <math>I_E</math> deriva dal moto di portatori in corrispondenza della regione svuotata tra emettitore e base;
- la corrente <math>I_C</math> deriva dal moto di portatori in corrispondenza della regione svuotata tra base e collettore.
Il flusso <math>{F_n}_{BC}</math> dei portatori maggioritari provenienti dall'emettitore si aggiunge ai flussi <math>{ {F_n}_{BC} }_0</math> e <math>{ {F_p}_{BC} }_0</math> di portatori minoritari che avrebbe il collettore se fosse isolato dall'emettitore, e che danno origine alla piccolissima corrente inversa di saturazione <math>{I_{CB}}_0</math>.
Parametri di efficienza del dispositivo a transistore[modifica | modifica sorgente]
5 Il comportamento da amplificatore è accentuabile minimizzando la corrente di ingresso <math>I_B</math>:
- <math>\begin{cases} I_B + I_C + I_E = 0 \\ I_B \approx 0 \end{cases} \Rightarrow I_C \approx - I_E</math>
12 cioè minimizzando il flusso di lacune maggioritarie <math>{F_p}_{BE}</math> tra base ed emettitore con un differente livello di drogaggio tra base ed emettitore:
- <math>\begin{cases} I_B = - I_C - I_E = qA {F_n}_{EB} + qA {F_n}_{BE} - qA {F_n}_{BC} \\ I_C \approx - I_E \\ {N_A}_B \ll {N_D}_E \Rightarrow {F_p}_{BE} \approx 0 \end{cases} \Rightarrow \begin{cases} I_B \approx 0 \\ {F_n}_{EB} \approx {F_n}_{BC} \end{cases}</math>
I fattori di merito del transistore sono due parametri che misurano la qualità del dispositivo, perché sono tanto più vicini a 1 quanto più è minimizzata la corrente di ingresso <math>I_B</math>:
- 16 la condizione <math>{F_p}_{BE} \approx 0</math> è misurata dall'efficienza di iniezione di emettitore <math>\gamma</math>:
- <math>\gamma = \frac{ {F_n}_{EB} }{ {F_n}_{EB} + {F_p}_{BE} } \leq 1</math>
- che per avvicinarsi all'idealità impone la seguente condizione sui livelli di drogaggio di base <math>{N_A}_B</math> ed emettitore <math>{N_D}_E</math>:[3]
- <math>\gamma = \frac{1}{1+ \frac{ {D_p}_E }{ {D_n}_B } \cdot \frac{ {N_A}_B }{ {N_D}_E } \cdot \frac{w_B}{w_E} } \to 1 \Leftrightarrow {N_A}_B \ll {N_D}_E</math>
- 12 la condizione <math>{F_n}_{EB} \approx {F_n}_{BC}</math> è misurata dal fattore di trasporto di base <math>b</math>:
- <math>b= \frac{ {F_n}_{BC} }{ {F_n}_{EB} } \leq 1</math>
- che per avvicinarsi all'idealità impone che la base sia un lato corto:
- <math>b= \frac{1}{ \cosh{ \frac{w_B}{ {L_n}_B } } } \to 0 \Leftrightarrow w_B \ll {L_n}_B</math>
Altri parametri descrivono l'efficienza del dispositivo:
- 13 l'amplificazione di corrente a base comune <math>\alpha_F</math>, idealmente pari a 1, lega la corrente <math>I_C</math> del collettore alla corrente <math>I_E</math> dell'emettitore:
- <math>\alpha_F = \gamma_b < 1 \Rightarrow I_C = - \alpha_F I_E + {I_{CB}}_0 \approx - \alpha_F I_E</math>
- dove la corrente inversa di saturazione <math>{I_{CB}}_0</math> è detta corrente di collettore a emettitore aperto (cioè se <math>I_E=0 \Rightarrow I_C= {I_{CB}}_0</math>);
- 14 l'amplificazione di corrente a emettitore comune <math>\beta_F</math>, idealmente molto grande,[4] lega la corrente <math>I_C</math> del collettore alla corrente <math>I_B</math> della base:
- <math>\beta_F = \frac{\alpha_F}{1- \alpha_F} \Rightarrow I_C = \beta_F I_B + {I_{CE}}_0</math>
- dove <math>{I_{CE}}_0</math> è la corrente di collettore a base aperta (<math>I_B=0</math>):
- <math>\begin{cases} {I_{CE}}_0 = \frac{\beta_F}{\alpha_F} {I_{CB}}_0 \\ \alpha_F \to 1 \end{cases} \Rightarrow \begin{cases} {I_{CE}}_0 \approx \beta_F {I_{CB}}_0 \\ {I_{CB}}_0 \approx 0 \end{cases} \Rightarrow I_C \approx \beta_F I_B</math>
Modello statico di Ebers Moll[modifica | modifica sorgente]
Configurazione a base comune[modifica | modifica sorgente]
18 Il modello statico di Ebers Moll generalizza il funzionamento in regione attiva diretta → vale in ogni regione di funzionamento indipendentemente dalla polarizzazione delle tensioni applicate:
- <math>\begin{cases} I_E = - I_F + \alpha_R I_R \\ I_C = - I_R + \alpha_F I_F \end{cases}</math>
dove:
- <math>I_F</math> e <math>I_R</math> sono le caratteristiche statiche delle singole giunzioni:
- <math>\begin{cases} I_F = {I_E}_0 \left( e^{\frac{ V_{BE} }{ V_T }} -1 \right) \\ I_R = {I_C}_0 \left( e^{\frac{ V_{BC} }{V_T}} -1 \right) \end{cases}</math>
- 19 <math>\alpha_R</math> è l'amplificazione di corrente a base comune in regione attiva inversa, legata ad <math>\alpha_F</math> dalla condizione di reciprocità:
- <math>\alpha_R {I_C}_0 = \alpha_F {I_E}_0</math>
Il circuito equivalente sostituisce a ogni giunzione il parallelo tra un diodo, rappresentante il flusso di corrente che la giunzione avrebbe se fosse isolata, e un generatore pilotato di corrente, rappresentante il contributo in corrente proveniente dall'altra giunzione:
- 20 regione attiva diretta: la corrente dei portatori minoritari della giunzione base-collettore <math>I_R</math> è trascurabile:
- <math>\begin{cases} I_E = - I_F \\ I_C = \alpha_F I_F \\ I_B = - I_C - I_E \end{cases} \Rightarrow \begin{cases} I_C \approx - \alpha_F I_E = \alpha_F {I_E}_0 \left( e^{\frac{V_{BE}}{V_T}} -1 \right) \\ I_B \approx \left( 1- \alpha_F \right) I_E \end{cases}</math>
- 21 regione attiva inversa: la corrente dei portatori minoritari della giunzione base-emettitore <math>I_E</math> è trascurabile:
- <math>\begin{cases} I_C = - I_R \\ I_E = \alpha_R I_R \end{cases} \Rightarrow I_E \approx - \alpha_R I_C</math>
Configurazione a emettitore comune[modifica | modifica sorgente]
26 Il modello statico di Ebers Moll descrive un transistore in configurazione a base comune:
- <math>\begin{cases} I_E = f \left( V_{BE} , V_{BC} \right) \\ I_C = f \left( V_{BE} , V_{BC} \right) \end{cases}</math>
Nella configurazione a emettitore comune, l'ingresso è la corrente <math>I_B</math> entrante nella base, e l'uscita è la corrente <math>I_C</math> entrante nel collettore. Il terminale in comune tra ingresso e uscita è l'emettitore, a cui fanno riferimento tutte le tensioni:
- <math>\begin{cases} I_B = f \left( V_{BE} , V_{CE} \right) \\ I_C = f \left( V_{BE} , V_{CE} \right) \end{cases}</math>
In regione attiva diretta (<math>V_{CE} \geq 0,2 \; V</math>):
- 27 la caratteristica di ingresso <math>I_B \left( V_{BE} , V_{CE} \right)</math>, per ogni tensione <math>V_{BE}</math> fissata, è indipendente dalla tensione <math>V_{CE}</math>, e quindi <math>V_{BC}</math>, applicata, 30 ed è approssimabile a una "spezzata" nel punto di accensione (<math>V_{BE} =0,5 \div 0,6 \; V</math> per il silicio);
- 28 la corrente di uscita <math>I_C \left( V_{BE} , V_{CE} \right)</math>, per ogni corrente di ingresso <math>I_B \left( V_{BE} , V_{CE} \right)</math> fissata, è indipendente dalla tensione <math>V_{CE}</math> applicata,[5] 31 ed è approssimabile con un "pettine" e con una resistenza finita in condizioni di saturazione.
Uso in commutazione (digitale)[modifica | modifica sorgente]
33 Il circuito in figura impone una retta di carico alla porta di uscita (collettore):
- <math>V_{CC} = R_C I_C+ V_{CE}</math>
32 Il transistore bipolare può essere usato nelle applicazioni digitali commutando, attraverso la scelta della corrente di ingresso <math>I_B</math>, tra la regione di saturazione (<math>V_{CE} = {V_{CE}}_{\text{sat}} \approx 0</math>) e quella di interdizione (<math>I_C=0</math>).
33 Il punto di funzionamento <math>\left( {I_C}_0 , {V_{CE}}_0 \right)</math> del transistore è l'intersezione tra la retta di carico e la caratteristica di uscita <math>I_C= \beta_F I_B</math>:
- interdizione (circuito aperto):
- <math>I_B \approx 0 \Rightarrow \begin{cases} {I_C}_0 \approx 0 \\ {V_{CE}}_0 \approx V_{CC} \end{cases}</math>
- saturazione/conduzione (cortocircuito):
- <math>I_B \geq \frac{ {I_C}_0 }{\beta_F} \Rightarrow \begin{cases} {I_C}_0 = \frac{V_{CC} - {V_{CE}}_{\text{sat}}}{R_C} \approx \frac{V_{CC}}{R_C} \\ {V_{CE}}_0 \approx {V_{CE}}_{\text{sat}} \end{cases}</math>
34 Più la corrente <math>I_B</math> è elevata, più si garantisce che la tensione <math>{V_{CE}}_0</math> sia compresa nella regione di saturazione (<math>{V_{CE}}_0 < {V_{CE}}_{\text{sat}}</math>), e più è bassa la potenza dissipata <math>P= {V_{CE}}_0 \cdot {I_C}_0 \leq {V_{CE}}_0 \cdot \left( {\beta_F}_{\text{min}} I_B \right)</math> → per massimizzare la corrente <math>I_B</math> così da minimizzare la tensione <math>{V_{CE}}_0</math>, conviene scegliere l'estremo inferiore <math>{\beta_F}_{\text{min}}</math> della fascia di incertezza di <math>\beta_F</math>.
Effetto Early[modifica | modifica sorgente]
35 In regione attiva diretta, a un aumento della tensione <math>V_{CE}</math> corrisponde un aumento[6] della tensione di polarizzazione inversa <math>V_{BC}</math> → la regione svuotata della giunzione base-collettore allarga i propri confini <math>x_p</math> e <math>x_n</math>, in particolare avvicinandosi all'emettitore dalla parte della base → aumenta il flusso di elettroni maggioritari provenienti dall'emettitore → 36 le caratteristiche di uscita <math>I_C \left( V_{CE} \right)</math> non sono più idealmente costanti al variare della tensione di uscita <math>V_{CE}</math>, 37 ma convergono alla tensione di Early <math>-V_A</math> con pendenza <math>\frac{ {I_C}_0}{V_A+ {V_C}_0}</math>.
35 Per minimizzare l'effetto Early, poiché vale la condizione di neutralità:
- <math>{N_A}_B x_p = {N_D}_C x_n \Rightarrow \frac{ {N_A}_B}{ {N_D}_C} = \frac{x_p}{x_n} = \text{cost.}</math>
si può minimizzare l'estensione del confine <math>x_p</math> nella base imponendo un differente livello di drogaggio tra base e collettore:
- <math>{N_A}_B \gg {N_D}_C</math>
in modo che la regione di svuotamento si estenda di più nel collettore dalla parte del confine <math>x_n</math>. 38 In definitiva:
- <math>{N_D}_E \gg {N_A}_B \gg {N_D}_C</math>
Fenomeni di breakdown[modifica | modifica sorgente]
38 L'allargamento della regione svuotata verso l'emettitore può portare al breakdown per perforazione diretta (la base "sfora" nella regione svuotata della giunzione base-emettitore) o per effetto valanga: si verifica quindi un forte aumento della tensione <math>V_{CE}</math> e della corrente di uscita <math>I_C</math>, e quindi della potenza dissipata.
Modello dinamico di Ebers Moll[modifica | modifica sorgente]
Modello dinamico di ampio segnale[modifica | modifica sorgente]
40-41 Il modello dinamico di ampio segnale aggiunge al modello statico di Ebers Moll:
- due coppie di condensatori (non lineari) in parallelo, che tengono conto degli effetti capacitivi di ritardo associati alle singole giunzioni (ovvero la capacità di svuotamento <math>C_s \left( v \right)</math> e la capacità di diffusione <math>C_d \left( v \right)</math>);
- tre resistenze parassite collegate ai tre terminali, che tengono conto delle perdite in prestazioni.
Modello statico[7] di piccolo segnale[modifica | modifica sorgente]
43 Scomponendo, linearizzando e approssimando in piccolo segnale le caratteristiche <math>I_C</math> e <math>I_B</math> della configurazione a emettitore comune, si trovano le espressioni del doppio bipolo transistore:
- <math>\begin{cases} {i_B}_{ss} \left( t \right) = {\left. \frac{\partial i_B}{\partial v_{BE}} \right|}_{\left( {V_{BE}}_0 , {V_{CE}}_0 \right)} {v_{BE}}_{ss} \left( t \right) + {\left. \frac{\partial i_B}{\partial v_{CE}} \right|}_{\left( {V_{BE}}_0 , {V_{CE}}_0 \right)} {v_{CE}}_{ss} \left( t \right) = g_{11} {v_{BE}}_{ss} \left( t \right) + g_{12} {v_{CE}}_{ss} \left( t \right) \\
{i_C}_{ss} \left( t \right) = {\left. \frac{\partial i_C}{\partial v_{BE}} \right|}_{\left( {V_{BE}}_0 , {V_{CE}}_0 \right)} {v_{BE}}_{ss} \left( t \right) + {\left. \frac{\partial i_C}{\partial v_{CE}} \right|}_{\left( {V_{BE}}_0 , {V_{CE}}_0 \right)} {v_{CE}}_{ss} \left( t \right) = g_{21} {v_{BE}}_{ss} \left( t \right) + g_{22} {v_{CE}}_{ss} \left( t \right) \end{cases}</math> 44 dove, in regione attiva diretta:
- <math>g_{11}</math> e <math>g_{22}</math> sono delle conduttanze:
- <math>\begin{cases} g_{11} = {\left. \frac{\partial i_B}{\partial v_{BE}} \right|}_{\left( {V_{BE}}_0 , {V_{CE}}_0 \right)} = \frac{g_{21}}{\beta_F} = \frac{ {I_C}_0 }{\beta_F V_T} \\
g_{22} = {\left. \frac{\partial i_C}{\partial v_{CE}} \right|}_{\left( {V_{BE}}_0 , {V_{CE}}_0 \right)} = \frac{ {I_C}_0 }{V_A + {V_C}_0} \approx \frac{ {I_C}_0 }{V_A} \end{cases}</math>
- <math>g_{12}</math> e <math>g_{21}</math> sono delle trans-conduttanze:
- <math>\begin{cases} g_{12} = {\left. \frac{\partial i_B}{\partial v_{CE}} \right|}_{\left( {V_{BE}}_0 , {V_{CE}}_0 \right)} = \frac{g_{22}}{\beta_F} \approx \frac{ {I_C}_0 }{\beta_F V_A} \\
g_{21} = {\left. \frac{\partial i_C}{\partial v_{BE}} \right|}_{\left( {V_{BE}}_0 , {V_{CE}}_0 \right)} = \frac{ {I_C}_0 }{V_T} \end{cases}</math>
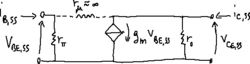
45 Le equazioni sono interpretabili circuitalmente come il circuito a π in figura, dove:
- <math>\begin{matrix} r_\pi = \frac{1}{g_{11}} = \beta_F \frac{V_T}{ {I_C}_0 } && r_o = \frac{1}{g_{22}} = \frac{V_A}{ {I_C}_0 } \\ r_\mu = \frac{1}{g_{12}} = \beta_F \frac{V_A}{ {I_C}_0 } && g_m = g_{21} = \frac{ {I_C}_0 }{V_T} \end{matrix}</math>
<math>g_m</math> è la transconduttanza del transistore nel suo punto di funzionamento a riposo, e lega la corrente di uscita <math>i_C</math> e la tensione di ingresso <math>V_{BE}</math> → per avere un'amplificazione elevata, il transistore va polarizzato con una corrente di collettore <math>{I_C}_0</math> elevata. In assenza di effetto Early, le resistenze <math>r_\mu</math> e <math>r_o</math> che modellizzano le perdite non hanno più influenza:
- <math>V_A \to + \infty \Rightarrow \begin{cases} r_\mu \to + \infty \\ r_o \to + \infty \end{cases}</math>
Modello dinamico di piccolo segnale[modifica | modifica sorgente]
46 Gli effetti capacitivi che tengono conto del comportamento dinamico sono dati dai contributi della capacità di svuotamento <math>C_s \left( v \right)</math> della giunzione base-collettore e della capacità di diffusione <math>C_d \left( v \right)</math> della giunzione base-emettitore. Ad alta frequenza, i condensatori si approssimano al cortocircuito → impediscono al dispositivo di funzionare.
Note[modifica | modifica sorgente]
- ↑ La porta è una coppia di terminali tali che la corrente che esce da uno entra dall'altro.
- ↑ Per i portatori maggioritari si assumono le ipotesi semplificative (condizioni stazionarie e fenomeni di generazione/ricombinazione trascurabili) → il loro contributo in corrente è esprimibile in funzione di quello dei portatori minoritari.
- ↑ La base e l'emettitore sono supposti essere lati corti.
- ↑ 15 Proprio perché <math>\beta_F</math> è un valore molto grande rispetto ad <math>\alpha_F</math> da cui deriva, l'errore di <math>\alpha_F</math> si propaga molto in <math>\beta_F</math>:
- <math>\frac{\Delta \beta_F}{\beta_F} \approx \beta_F \frac{\Delta \alpha_F}{\alpha_F}</math>
- ↑ Anche in regione attiva inversa la corrente di uscita è indipendente, ma essa risulta amplificata molto meno.
- ↑ in valore assoluto
- ↑ Il modello statico è approssimativamente valido, oltre che per il punto di funzionamento a riposo, anche per segnali tempo-varianti a basse frequenze, poiché si possono trascurare gli effetti capacitivi.