Teoria ed elaborazione dei segnali/Campionamento
| A8. Spettro di energia e segnali troncati |
2 Un segnale analogico è più facile da elaborare se viene campionato in un segnale numerico, cioè tempo discreto e discreto in ampiezza. Come campionare un segnale tempo-continuo senza perdere informazione?
- Teorema del campionamento (o di Nyquist-Shannon)
Un segnale tempo-continuo può essere campionato e perfettamente ricostruito a partire dai suoi campioni se la frequenza di campionamento <math>f_c</math> è maggiore del doppio della banda[1] <math>B</math> del segnale:
- <math>f_c \triangleq \frac{1}{T_c} > 2B</math>
5 con la condizione che la banda <math>B</math> sia limitata.
3 Il teorema del campionamento garantisce che il segnale campionato può essere ricostruito perfettamente tramite un filtro interpolatore (ricostruttore), e che il segnale ricostruito coinciderà con il segnale tempo-continuo di partenza.
Filtro anti-aliasing[modifica | modifica sorgente]
8-9-10 La maggioranza dei segnali utilizzati nella realtà ha banda illimitata: esiste un intervallo al di fuori del quale il segnale è significativamente vicino a zero, ma non è mai identicamente nullo. Il segnale campionato quindi presenterà nel dominio della frequenza delle sovrapposizioni degli spettri che alla fine non possono essere ricostruite dal filtro interpolatore. Il filtro anti-aliasing serve per eliminare le parti ad alta frequenza prima del campionamento:
- <math>\mathrm{AA} \left( f \right) \begin{cases} = 0 & \left| f \right| > B_{\mathrm{AA}} \\
\neq 0 & \text{altrove} \end{cases}</math> con <math>B_x < B_{\mathrm{AA}} < \tfrac{f_c}{2}</math>. La distorsione del filtro anti-aliasing non è ugualmente rimediabile, ma è comunque preferibile rispetto all'effetto di aliasing (o sovrapposizione).
Campionatori reali[modifica | modifica sorgente]
11-12 Il campionatore ideale (treno di delta):
- <math>x ' \left( t \right) = x \left( t \right) * \delta \left( - t \right) = \sum_{n = - \infty}^{+ \infty} \delta \left( t - n T_c \right) x \left( t \right)</math>
è impossibile da realizzare nella realtà, perché la delta <math>\delta \left( t \right)</math> è un impulso con ampiezza illimitata e supporto infinitesimo → si utilizza un impulso <math>h \left( t \right)</math> il più possibile simile alla delta, cioè con ampiezza molto grande e supporto molto piccolo:
- <math>x ' \left( t \right) = x \left( t \right) * h \left( - t \right) \Rightarrow x ' \left( n T_c \right) = \int_{- \infty}^{+ \infty} h \left( \tau - n T_c \right) x \left( \tau \right) d \tau</math>
Interpolatori[modifica | modifica sorgente]
Condizioni ideali[modifica | modifica sorgente]
4-5 Un segnale campionato:
- <math>\begin{cases} x_c \left( t \right) = \sum_{n = - \infty}^{+ \infty} x \left( n T_c \right) \delta \left( t - n T_c \right) \\
X_c \left( f \right) = \frac{1}{T_c} \sum_{n = - \infty}^{+ \infty} X \left( f - \frac{n}{T_c} \right) \end{cases}</math> può essere ricostruito tramite un filtro passa-basso ideale, detto filtro ricostruttore ottimo <math>K \left( f \right)</math>:
- <math>x \left( t \right) = x_c \left( t \right) * K \left( t \right) = \left[ \sum_{n = - \infty}^{+ \infty} x \left( n T_c \right) \delta \left( t - n T_c \right) \right] * K \left( t \right) = \sum_{n = - \infty}^{+ \infty} x \left( n T_c \right) K \left( t - n T_c \right) , \quad K \left( f \right ) = \begin{cases} T_c & \left| f \right| < B \\
\text{qualsiasi valore} & B < \left| f \right| < f_c - B \\ 0 & \left| f \right| > f_c - B \end{cases}</math>
Il filtro ricostruttore ottimo <math>K \left( f \right)</math> deve essere:
- non distorcente nella banda del segnale (piatto);
- nullo al di fuori della banda del segnale per eliminare le componenti ad alta frequenza.
Esempi di interpolatori distorcenti[modifica | modifica sorgente]
- 6 Costante a tratti
Il segnale viene approssimato a una serie di rettangoli:
- <math>\begin{cases} K \left( t \right) = {\Pi}_{T_c} \left( t \right) \\
K \left( f \right) = T_c \mathrm{sinc} \left( f T_c \right) \end{cases}</math>
- Lineare
Il segnale viene approssimato a una serie di trapezi:
- <math>\begin{cases} K \left( t \right) = {\Lambda}_{T_c} \left( t \right) \\
K \left( f \right) = T_c {\mathrm{sinc}}^2 \left( f t_c \right) \end{cases}</math>
Esempi di interpolatori non distorcenti[modifica | modifica sorgente]
- 7 Funzione sinc
Il filtro interpolatore ideale è il seguente:
- <math>\begin{cases} K \left( t \right) = B T_c \mathrm{sinc} \left( t B \right) \\
K \left( f \right) = T_c \Pi_B \left( f \right) \end{cases}</math> perché il segnale viene ricostruito da una sommatoria di infinite funzioni sinc, dove per ogni <math>n</math> esiste una sinc che assume esattamente il valore del campione <math>n</math>-esimo all'istante <math>n T_c</math> e un valore nullo in tutti gli altri istanti di campionamento:
- <math>x \left( t \right) = B T_c \sum_{n = - \infty}^{+ \infty} x \left( n T_c \right) \mathrm{sinc} \left( B \left( t - n T_c \right) \right)</math>
Tuttavia nei punti intermedi agli istanti di campionamento il segnale <math>x \left( t \right)</math> è dato dalla somma dei contributi di infinite funzioni sinc:
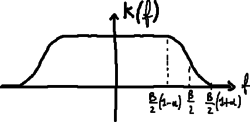
- Coseno rialzato
- <math>K \left( t \right) = N T_c \mathrm{sinc} \left( Bt \right) \cdot \frac{\cos{\alpha B \pi t}}{1 - {\alpha B t}^2}</math>
Condizioni:
- roll-off <math>\alpha</math>: <math>0 < \alpha < 1</math> (se <math>\alpha = 0</math> diventa la funzione sinc)
- <math>\frac{B}{2} \left( 1 - \alpha \right) > B_x</math>
- <math>\frac{B}{2} \left( 1 + \alpha \right) < f_c - B_x</math>
Condizioni reali[modifica | modifica sorgente]
12-13 Il filtro ricostruttore può integrare anche un filtro equalizzatore che rimedi agli effetti del filtro anti-aliasing e alle distorsioni provocate da un campionatore reale:
- <math>K \left( f \right) = \begin{cases} \frac{T_c}{\mathrm{AA} \left( f \right) H \left( f \right)} & \left| f \right| < B_{\mathrm{AA}} \\
0 & \left| f \right| > f_c - B_{\mathrm{AA}} \end{cases}</math> a patto che <math>H \left( f \right)</math>, cioè la trasformata di Fourier dell'impulso campionatore <math>h \left( t \right)</math>, non cancelli definitivamente qualche frequenza compresa nella banda <math>B_{\mathrm{AA}}</math> del filtro anti-aliasing:
- <math>H \left( f \right) \neq 0 \quad \forall \left| f \right| < B_{\mathrm{AA}}</math>
Note[modifica | modifica sorgente]
- ↑ Per banda si intende qui la lunghezza del supporto in frequenza.
| A8. Spettro di energia e segnali troncati |