Teoria ed elaborazione dei segnali/Trasformata di Fourier a tempo discreto
| B4. DFT e FFT |
Trasformata di Fourier a tempo discreto (DTFT)[modifica | modifica sorgente]
Definizione di DTFT[modifica | modifica sorgente]
7-9 La trasformata di Fourier a tempo discreto (DTFT) <math>X \left( e^{j2 \pi f} \right)</math> è la trasformata di Fourier della sequenza <math>x \left( n \right)</math>:
- <math>X \left( e^{j2 \pi f} \right) = \mathcal{F} \left\{ x \left( n \right) \right\} = \sum_{k = - \infty}^{+ \infty} x \left( k \right) e^{-j2 \pi f k} = \sum_{k = - \infty}^{+ \infty} x \left( k \right) e^{-j \omega k}</math>
dove <math>\omega</math> è la pulsazione discreta: <math>\omega = 2 \pi f</math>.
8 La DTFT viene indicata con <math>X \left( e^{j2 \pi f} \right)</math> anziché con <math>X \left( f \right)</math> per distinguerla dalla trasformata di Fourier di un segnale continuo, ma è a tutti gli effetti in funzione della variabile continua <math>f</math>.
7 La DTFT è in realtà il caso particolare per <math>T_c = 1</math> della trasformata di Fourier di un segnale analogico <math>x \left( t \right)</math> campionato con frequenza di campionamento <math>f_c = \frac{1}{T_c}</math>:
- <math>X_c \left( f \right) = \mathcal{F} \left\{ \sum_{k = - \infty}^{+ \infty} x \left( k T_c \right) \delta \left( t - k T_c \right) \right\} = \sum_{k = - \infty}^{+ \infty} x \left( k T_c \right) e^{-j2 \pi f k T_c}</math>
8 che è periodica di periodo <math>f_c</math> → la DTFT è periodica di periodo:
- <math>\begin{cases} f_c = \frac{1}{T_c} = 1 \\
\omega = 2 \pi f_c = 2 \pi \end{cases}</math>
Inversione della DTFT (IDTFT)[modifica | modifica sorgente]
10-11 Siccome la DTFT <math>X \left( e^{j \omega} \right)</math> è periodica, i coefficienti <math>x \left( k \right)</math> possono essere interpretati come i coefficienti <math>\mu_k</math> dello sviluppo in serie di Fourier della DTFT:
| Tempo continuo | Tempo discreto | |
|---|---|---|
| in funzione di <math>f</math> | in funzione di <math>\omega</math> | |
| <math>x \left( t \right) = \sum_{k = - \infty}^{+ \infty} \mu_k e^{j \frac{2 \pi}{T} kt}</math> <math>\mu_k = \frac{1}{T} \int_{- \frac{T}{2}}^{+ \frac{T}{2}} x \left( t \right) e^{-j \frac{2 \pi}{T} k t} dt</math> |
<math>X \left( e^{j 2 \pi f} \right) = \sum_{k = - \infty}^{+ \infty} x \left( k \right) e^{-j 2 \pi f k}</math> <math>x \left( k \right) = \int_{- \frac{1}{2}}^{+ \frac{1}{2}} X \left( e^{j 2 \pi f} \right) e^{j2 \pi f k} df</math> |
<math>X \left( e^{j \omega} \right) = \sum_{k = - \infty}^{+ \infty} x \left( k \right) e^{-j \omega k}</math> <math>x \left( k \right) = \frac{1}{2 \pi} \int_{- \pi}^{+ \pi} X \left( e^{j \omega} \right) e^{j \omega k} d \omega</math> |
- <math>\int_{- \frac{1}{2
^{+ \frac{1}{2}} X \left( e^{j 2 \pi f } \right) e^{j2 \pi f k} df = \int_{- \frac{1}{2}}^{+ \frac{1}{2}} \left[ \sum_{n = - \infty}^{+ \infty} x \left( n \right) e^{-j2 \pi f n} \right] e^{j2 \pi f k} df = \sum_{n = - \infty}^{+ \infty} x \left( n \right) \int_{- \frac{1}{2}}^{+ {1 \over 2}} e^{-j 2 \pi f \left( n - k \right)} df = \sum_{n = - \infty}^{+ \infty} x \left( n \right) \frac{1}{-j2 \pi \left( n - k \right)} \left. e^{-j2 \pi f \left( n - k \right)} \right \vert_{- \frac{1}{2}}^{+ \frac{1}{2}} = \sum_{n = - \infty}^{+ \infty} x \left( n \right) \frac{1}{j 2 \pi \left( n - k \right)} \left( e^{j \pi \left( n - k \right)} - e^{-j \pi \left( n - k \right)} \right) =</math>
Per la formula di Eulero:
- <math>= \sum_{n = - \infty}^{+ \infty} x \left( n \right) \frac{\sin \left( \pi \left( n - k \right) \right)}{\pi \left( n - k \right)} = \sum_{n = - \infty}^{+ \infty } x \left( n \right) \mathrm{sinc} \left( n - k \right) = \sum_{n = - \infty}^{+ \infty} x \left( n \right) \delta \left( n - k \right) = x \left( k \right)</math>
}}
Condizioni di esistenza[modifica | modifica sorgente]
Se la sequenza <math>x \left( k \right)</math> è assolutamente sommabile, allora:
- 14 esiste la sua DTFT:
- <math>\sum_{k = - \infty}^{+ \infty} \left| x \left( k \right) \right| \in \R \Rightarrow \left| X \left( e^{j \omega} \right) \right| \in \R \quad \forall \omega</math>
- <math>\left
- 15 la sua energia è finita:
- <math>\sum_{k = - \infty}^{+ \infty} \left| x \left( k \right) \right| \in \R \Rightarrow E_x = \sum_{k = - \infty}^{+ \infty} {\left| x \left( k \right) \right|}^2 \in \R</math>
Proprietà della DTFT[modifica | modifica sorgente]
Linearità[modifica | modifica sorgente]
19 La DTFT è un operatore lineare:
- <math>z \left( n \right) = a_1 \cdot x \left( n \right) + a_2 \cdot y \left( n \right) \Longleftrightarrow Z \left( e^{j 2 \pi f} \right) = a_1 \cdot X \left( e^{j 2 \pi f} \right) + a_2 \cdot Y \left( e^{j 2 \pi f} \right)</math>
Ribaltamento[modifica | modifica sorgente]
20 Un ribaltamento della <math>x \left( n \right)</math> corrisponde a calcolare la sua DTFT invertendo il segno della frequenza <math>f</math>:
- <math>z \left( n \right) = x \left( - n \right) \Longleftrightarrow Z \left( e^{j 2 \pi f} \right) = X \left( e^{- j 2 \pi f} \right)</math>
Ritardo[modifica | modifica sorgente]
21 Una traslazione del tempo della sequenza <math>x \left( n \right)</math> corrisponde a moltiplicare la sua DTFT per un esponenziale complesso:
- <math>z \left( n \right) = x \left( n - N \right) \Longleftrightarrow Z \left( e^{j 2 \pi f} \right) = X \left( e^{j 2 \pi f} \right) e^{- j 2 \pi f N}</math>
Traslazione in frequenza (modulazione)[modifica | modifica sorgente]
22 Una traslazione in frequenza della DTFT di una sequenza <math>x \left( n \right)</math> corrisponde a moltiplicare la sequenza per un esponenziale complesso:
- <math>z \left( n \right) = x \left( n \right) \cdot e^{j 2 \pi f_0 n} \Longleftrightarrow Z \left( e^{j 2 \pi f } \right) = X \left( e^{j 2 \pi \left( f - f_0 \right)} \right)</math>
Derivazione in frequenza[modifica | modifica sorgente]
23
- <math>z \left( n \right) = n \cdot x \left( n \right) \Longleftrightarrow - 2 \pi j \cdot Z \left( e^{j 2 \pi f} \right) = \frac{d }{df} X \left( e^{j 2 \pi f} \right)</math>
Convoluzione lineare[modifica | modifica sorgente]
24 La convoluzione tra due sequenze <math>x \left( n \right)</math> e <math>y \left( n \right)</math> corrisponde al prodotto tra le singole DTFT:
- <math>z \left( n \right) = x \left ( n \right) * y \left( n \right) = \sum_{k = - \infty}^{+ \infty} x \left( k \right) y \left( n - k \right) \Longleftrightarrow Z \left( e^{j 2 \pi f } \right) = X \left( e^{j2 \pi f} \right) \cdot Y \left( e^{j2 \pi f} \right)</math>
Prodotto[modifica | modifica sorgente]
25 Il prodotto tra due sequenze <math>x \left( n \right)</math> e <math>y \left( n \right)</math> corrisponde alla convoluzione tra le singole DTFT, con estremi di integrazione <math>- \tfrac{1}{2}</math> e <math>+ \tfrac{1}{2}</math> grazie al fatto che la DTFT è periodica:
- <math>z \left( n \right) = x \left( n \right) \cdot y \left( n \right) \Longleftrightarrow Z \left( e^{j 2 \pi f} \right) = X \left( e^{j 2 \pi f} \right) * Y \left( e^{j2 \pi f} \right) = \int_{- \frac{1}{2}}^{+ \frac{1}{2}} X \left( e^{j 2 \pi \eta} \right) Y \left( e^{j2 \pi \left( f - \eta \right) } \right) d \eta</math>
Relazioni di parità[modifica | modifica sorgente]
28 Se la sequenza <math>x \left( n \right)</math> è reale vale la simmetria hermitiana per le sue DTFT attorno alle frequenze <math>f = 0</math> e <math>f = \tfrac{1}{2}</math>:
- <math>\begin{cases} X \left( e^{j 2 \pi f} \right) = X^* \left( e^{-j2 \pi f} \right) \\
X \left( e^{j 2 \pi \left( f - \frac{1}{2} \right)} \right) = X^* \left( e^{- j 2 \pi \left( f + \frac{1}{2} \right)} \right) \end{cases} \Rightarrow \begin{cases} X_R \left( e^{j2 \pi f} \right) + j X_I \left( e^{j 2 \pi f } \right) = X_R \left( e^{-j2 \pi f} \right) - j X_I \left( e^{-j2 \pi f} \right) \\ X_R \left( e^{j2 \pi \left( f - \frac{1}{2} \right)} \right) + j X_I \left( e^{j 2 \pi \left( f - \frac{1}{2} \right) } \right) = X_R \left( e^{-j2 \pi \left( f + \frac{1}{2} \right)} \right) - j X_I \left( e^{-j2 \pi \left( f + \frac{1}{2} \right)} \right) \end{cases}</math> e quindi entrambe le DTFT hanno le seguenti relazioni di parità:
- 27 la parte reale è pari:
- <math>\begin{cases} X_R \left( e^{j 2 \pi f} \right) = X_R \left( e^{- j 2 \pi f} \right) \\ X_R \left( e^{j 2 \pi \left( f - \frac{1}{2} \right)} \right) = X_R \left( e^{- j 2 \pi \left( f + \frac{1}{2} \right)} \right) \end{cases}</math>
- 29 la parte immaginaria è dispari:
- <math>\begin{cases} X_I \left( e^{j 2 \pi f} \right) = - X_I \left( e^{- j 2 \pi f} \right) \\ X_I \left( e^{j 2 \pi \left( f - \frac{1}{2} \right)} \right) = - X_I \left( e^{- j 2 \pi \left( f + \frac{1}{2} \right)} \right) \end{cases}</math>
- il modulo è pari:
- <math>\begin{cases} {\left| X \left( e^{j 2 \pi f} \right) \right|}^2 = X_R^2 \left( e^{j 2 \pi f} \right) + X_I^2 \left( e^{j 2 \pi f} \right) \\
{\left| X \left( e^{j 2 \pi \left( f - \frac{1}{2} \right)} \right) \right|}^2 = X_R^2 \left( e^{j 2 \pi \left( f - \frac{1}{2} \right)} \right) + X_I^2 \left( e^{j 2 \pi \left( f - \frac{1}{2} \right)} \right) \end{cases}</math>
- la fase è dispari:
- <math>\begin{cases} \arg{X_I \left( e^{j2 \pi f} \right)} = \mathrm{arctg} \frac{X_I \left( e^{j2 \pi f} \right)}{X_R \left( e^{j2 \pi f} \right)} \\
\arg{X_I \left( e^{j2 \pi \left( f - \frac{1}{2} \right)} \right)} = \mathrm{arctg} \frac{X_I \left( e^{j2 \pi \left( f - \frac{1}{2} \right)} \right)}{X_R \left( e^{j2 \pi \left( f - \frac{1}{2} \right)} \right)} \end{cases}</math>
Valore iniziale e somma dei campioni[modifica | modifica sorgente]
- 37 Valore iniziale
- <math>\left. x \left( n \right) \right \vert_{n = 0} = x \left( 0 \right) = \int_{- \frac{1}{2}}^{+ \frac{1}{2}} X \left( e^{j 2 \pi f} \right) df</math>
- Somma dei campioni
- <math>\left. X \left( e^{j2 \pi f} \right) \right \vert_{f = 0} = \sum_{k = - \infty}^{+ \infty} x \left( k \right)</math>
Ne consegue che sequenze a valor medio nullo hanno DTFT nulla in <math>f = 0</math>.
Relazione di Parseval[modifica | modifica sorgente]
39 La relazione di Parseval nel dominio del tempo discreto ha estremi di integrazione finiti:
- <math>E_x = \sum_{k = - \infty}^{+ \infty} {\left| x \left( k \right) \right|}^2 = \int_{- \frac{1}{2}}^{+ \frac{1}{2}} {\left| X \left( e^{j2 \pi f} \right) \right|}^2 df</math>
- Relazione di Parseval generalizzata
- <math>\sum_{k = - \infty}^{+ \infty} x \left( k \right) y^* \left( k \right) = \int_{- \frac{1}{2}}^{+ \frac{1}{2}} X \left( e^{j2 \pi f} \right) Y^* \left( e^{j2 \pi f} \right) df</math>
Spettro di energia[modifica | modifica sorgente]
40 Lo spettro di energia <math>S_x \left( f \right)</math> dà informazioni sulla distribuzione dell'energia della sequenza <math>x \left( n \right)</math> nel dominio della frequenza:
- <math>S_x \left( f \right) = {\left| X \left( e^{j2 \pi f} \right) \right|}^2</math>
- Proprietà
Lo spettro di energia <math>S_x \left( f \right)</math>:
- non può essere negativo;
- se <math>x \left( n \right)</math> è reale, è reale e pari;
- è periodico di periodo 1.
DTFT notevoli[modifica | modifica sorgente]
| Sequenza <math>x \left( n \right)</math> | DTFT <math>X \left( e^{j 2 \pi f} \right)</math> | |
|---|---|---|
| 43 Sequenza delta | <math>\delta \left( n \right)</math> | <math>1</math> |
| Sequenza costante | <math>1</math> | <math>\sum_{n = - \infty}^{+ \infty} \delta \left( f - n \right)</math> <math>\delta \left( f \right) \quad f \in \left[ - \frac{1}{2} , \frac{1}{2} \right]</math> |
| 44 Sequenza segno | <math>\sgn \left( n \right)</math> | <math>\frac{1 + e^{-j 2 \pi f}}{1 - e^{-j2 \pi f}}</math> |
| 46 Sequenza gradino | <math>u \left( n \right)</math> | <math>\frac{1}{2} \delta \left( f \right) + \frac{1}{1 - e^{-j2 \pi f}}</math> |
| 47 Sequenza esponenziale | <math>e^{j2 \pi f_0 n}</math> | <math>\delta \left( f - f_0 \right)</math> |
| Sequenza cosinusoidale | <math>\cos \left( 2 \pi f_0 n \right)</math> | <math>\frac{1}{2} \left[ \delta \left( f - f_0 \right) + \delta \left( f + f_0 \right) \right]</math> |
| Sequenza sinusoidale | <math>\sin \left( 2 \pi f_0 n \right)</math> | <math>\frac{1}{2j} \left[ \delta \left( f - f_0 \right) - \delta \left( f + f_0 \right) \right]</math> |
| 48 Sequenza sinc | <math>\mathrm{sinc} \left( \frac{n}{N} \right)</math> | <math>N \cdot P_{\frac{1}{N}} \left( f \right)</math> |
| 49 Sequenza porta | <math>p_{2K+1} \left( n \right)</math> | <math>\frac{\sin \left[ \pi f \left( 2K + 1 \right) \right]}{\sin \left( \pi f \right)}</math> |
Banda di un segnale a tempo discreto[modifica | modifica sorgente]
Banda assoluta[modifica | modifica sorgente]
53 La banda assoluta della sequenza <math>x \left( n \right)</math> è la frequenza <math>B_x \leq \frac{1}{2}</math>, quindi all'interno del singolo periodo della DTFT, per cui la DTFT <math>\left| X \left( e^{j2 \pi f} \right) \right|</math> è identicamente nulla al di fuori dell'intervallo <math>\left[ - B_x, B_x \right]</math>. È l'equivalente della banda unilatera nel dominio del tempo discreto, però si considera solamente un periodo della funzione nel dominio della frequenza (la DTFT ha sempre supporto infinito).
Banda equivalente[modifica | modifica sorgente]
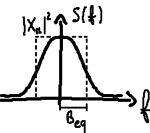
54 La larghezza di banda <math>B_{\text{eq}}</math> è pari alla semilarghezza del rettangolo:
- la cui altezza è pari al massimo <math>{\left| X_M \right|}^2</math> dello spettro di energia <math> S_x \left( f \right)</math>;
- la cui area è uguale all'energia complessiva <math>E \left( S_x \right)</math> della DTFT, cioè all'area sottesa da <math>S_x \left( f \right)</math> all'interno del singolo periodo della DTFT:
- <math>2 B_{\text{eq}} {\left| X_M \right|}^2 = \int_{- \frac{1}{2}}^{+ {1 \over 2}} S_x \left( f \right) df = \int_{- \frac{1}{2}}^{+ {1 \over 2}} {\left| X \left( e^{2j \pi f} \right) \right|}^2 df</math>
- che per la relazione di Parseval è anche uguale all'energia della sequenza <math>x \left( n \right)</math>, data dalla somma di tutti i suoi campioni:
- <math>2 B_{\text{eq}} {\left| X_M \right|}^2 = E_x = \sum_{k = - \infty}^{+ \infty} x \left( k \right)</math>
Banda Bx%[modifica | modifica sorgente]
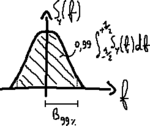
55 La banda <math>B_{x%}</math> è la frequenza per cui l'intervallo <math>\left[ - B_{x%} , B_{x%} \right]</math> corrisponde all'<math>x%</math> dell'energia complessiva della sequenza <math>y \left( n \right)</math>, ovvero all'<math>x%</math> dell'area sottesa dallo spettro di energia <math>S_y \left( f \right)</math> all'interno del singolo periodo della DTFT:
- <math>\int_{- B_{x%}}^{+ B_{x%}} S_y \left( f \right) df = \frac{x}{100} \int_{- {1 \over 2}}^{+ {1 \over 2}} S_y \left( f \right) df = \frac{x}{100} \sum_{k = - \infty}^{+ \infty} {\left| y \left( n \right) \right|}^2</math>
Banda a 3 dB[modifica | modifica sorgente]
56 La banda a 3 dB <math>B_{3 \text{ dB}}</math> è la frequenza a cui l'ampiezza dello spettro di energia <math>S_x \left( f \right)</math> si riduce di 3 dB rispetto al suo massimo:
- <math>S_x \left( B_{3 \text{ dB}} \right) = \frac{{\left| X_M \right| }^2}{2}</math>
| B4. DFT e FFT |