Controlli automatici/Stabilità interna di sistemi dinamici
| C15. Stabilità interna di sistemi dinamici LTI |
4 Lo studio della stabilità interna riguarda gli effetti sul movimento dello stato provocati da perturbazioni dello stato iniziale (l'ingresso rimane costante).
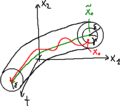
7 Considerando due evoluzioni temporali dello stato di un sistema dinamico stazionario:
- movimento nominale dello stato <math>\tilde x ( \bullet )</math>: ingresso nominale <math>\tilde u ( \bullet )</math>, stato iniziale nominale <math>{\tilde x}_0</math>;
- movimento perturbato dello stato <math>x ( \bullet )</math>: ingresso <math>u ( \bullet ) = \tilde u ( \bullet )</math>, stato iniziale <math>x_0 \neq {\tilde x}_0</math>.
la perturbazione <math>\delta x ( \bullet )</math> dello stato del sistema è la differenza tra i due movimenti, ed è tanto più piccola quanto meno il movimento perturbato si discosta dal movimento nominale:
- <math>\delta x ( \bullet ) = x ( \bullet ) - \tilde x (\bullet ) \in {\R}^n</math>
5 Un sistema è stabile se il suo movimento non si discosta troppo dal movimento nominale di riferimento a fronte di una piccola perturbazione dello stato iniziale.
Classificazione in base alla stabilità interna[modifica | modifica sorgente]
8 A fronte di una perturbazione <math>\delta x_0 = x_0 - {\tilde x}_0</math> dello stato iniziale, il movimento nominale <math>\tilde x ( \bullet )</math> è:
- 20 instabile se la perturbazione <math>\delta x( \bullet )</math> dello stato non resta limitata nel tempo (tipicamente diverge):
- <math>\forall \gamma > 0 : \; \exists \varepsilon > 0 \longrightarrow \exists x_0 : \; \left\| \delta x_0 \right\| \leq \gamma \Longrightarrow \exists t \geq 0 : \; \left\| \delta x \left( t \right) \right\| > \varepsilon</math>
- 14 stabile se la perturbazione <math>\delta x( \bullet )</math> dello stato resta limitata nel tempo:
- 28 semplicemente stabile se la perturbazione <math>\delta x( \bullet )</math> dello stato resta limitata, ma non tende a 0 asintoticamente:
- <math>\forall \varepsilon > 0 : \; \exists \gamma > 0 \longrightarrow \forall x_0 : \; \left\| \delta x_0 \right\| \leq \gamma \Longrightarrow \begin{cases} \left\| \delta x \left( t \right) \right\| \leq \varepsilon , \quad \forall t \geq 0 \\ \lim_{t \to + \infty} \left\| \delta x( t) \right\| = 0 \end{cases}</math>
- 26 asintoticamente stabile se la perturbazione <math>\delta x( \bullet )</math> dello stato resta limitata, e tende a 0 asintoticamente:
- <math>\forall \varepsilon > 0 : \; \exists \gamma > 0 \longrightarrow \forall x_0 : \; \left\| \delta x_0 \right\| \leq \gamma \Longrightarrow \begin{cases} \left\| \delta x \left( t \right) \right\| \leq \varepsilon , \quad \forall t \geq 0 \\ \lim_{t \to + \infty} \left\| \delta x( t) \right\| \neq 0 \end{cases}</math>
- 27 globalmente asintoticamente stabile se il movimento nominale <math>\tilde x ( \bullet )</math> è asintoticamente stabile per qualsiasi perturbazione iniziale:
- <math>\forall \varepsilon > 0 : \; \exists \gamma > 0 \longrightarrow \forall x_0 : \; \left\| \delta x_0 \right\| \leq \gamma \Longrightarrow \begin{cases} \left\| \delta x \left( t \right) \right\| \leq \varepsilon , \quad \forall t \geq 0 \\ \lim_{t \to + \infty} \left\| \delta x( t) \right\| \neq 0 , \quad \forall \delta x_0 \in X \end{cases}</math>
- 28 semplicemente stabile se la perturbazione <math>\delta x( \bullet )</math> dello stato resta limitata, ma non tende a 0 asintoticamente:
Stabilità dell'equilibrio[modifica | modifica sorgente]
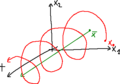
35 Se il movimento nominale considerato è un punto di equilibrio <math>\left( \bar x , \bar u \right)</math>, si studia la stabilità dell'equilibrio a fronte di perturbazioni dello stato iniziale (l'ingresso rimane pari all'ingresso di equilibrio <math>\bar u</math> costante). Ad ogni stato di equilibrio asintoticamente stabile è associata una regione di attrazione o regione di asintotica stabilità: ogni stato iniziale che appartiene alla regione di attrazione dà origine a un movimento perturbato che è asintoticamente stabile.
| C15. Stabilità interna di sistemi dinamici LTI |